こんにちは!
今日もキラーナンプレの最高難易度「エキスパート」を攻略していきます!
前回のキラーナンプレ攻略はコチラ ⇒【エキスパート】キラーナンプレ攻略1回目

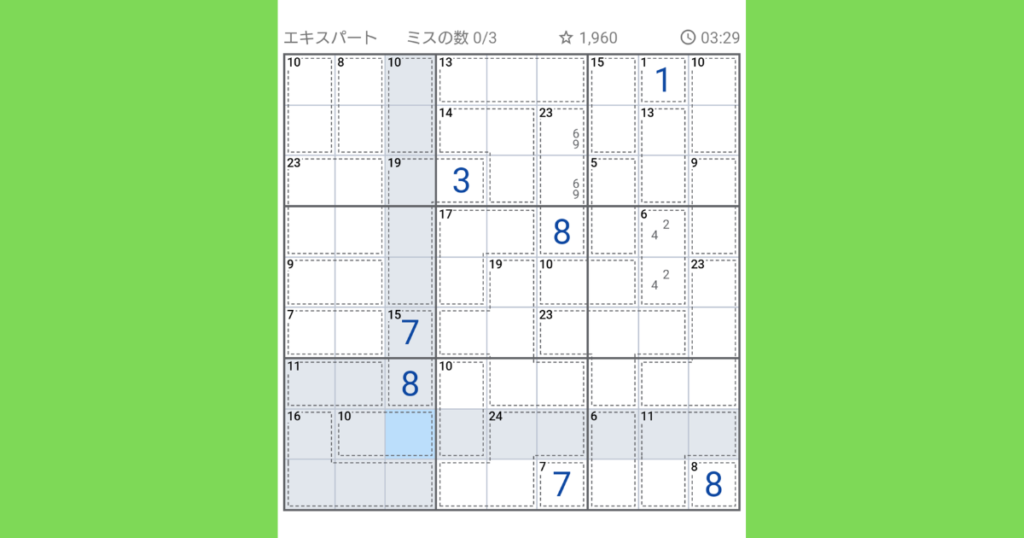
まずは上図で埋められる所を埋めていきます。【1】【7】【8】と、【23(3ブロック)】は(6,8,9)の組み合わせになります。
【1】と同じ列に【6(2ブロック)】がありますが、(1,5)、(2,4)の組み合わせしか無いのと上に1があるので(2,4)になります。
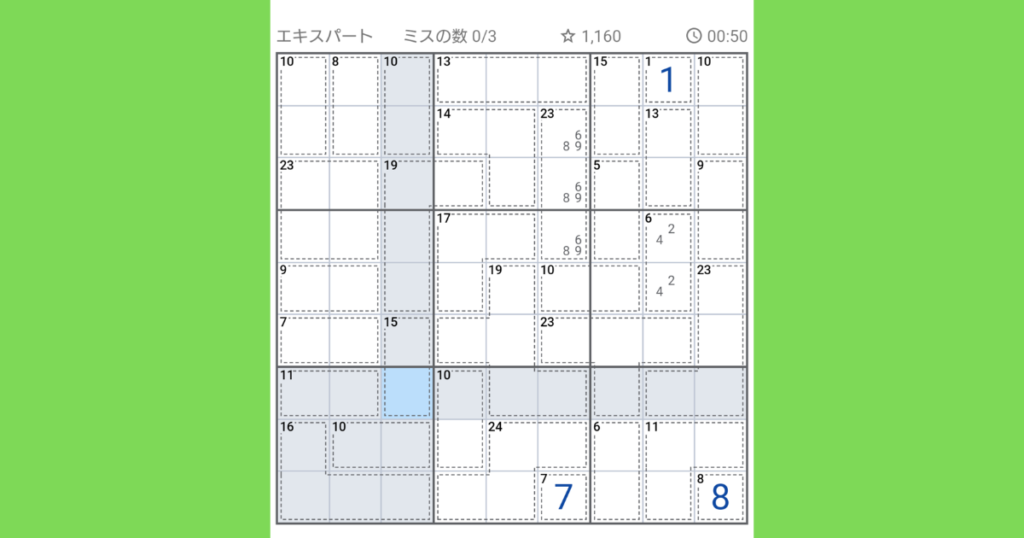
左下のブロックに注目します。全体の合計で45になりますが、【11(2ブロック)】【10(2ブロック)】【16(4ブロック)】があるので、残りの1マスが分かります。
45-(11+10+16)=8になるので、8が入ります。
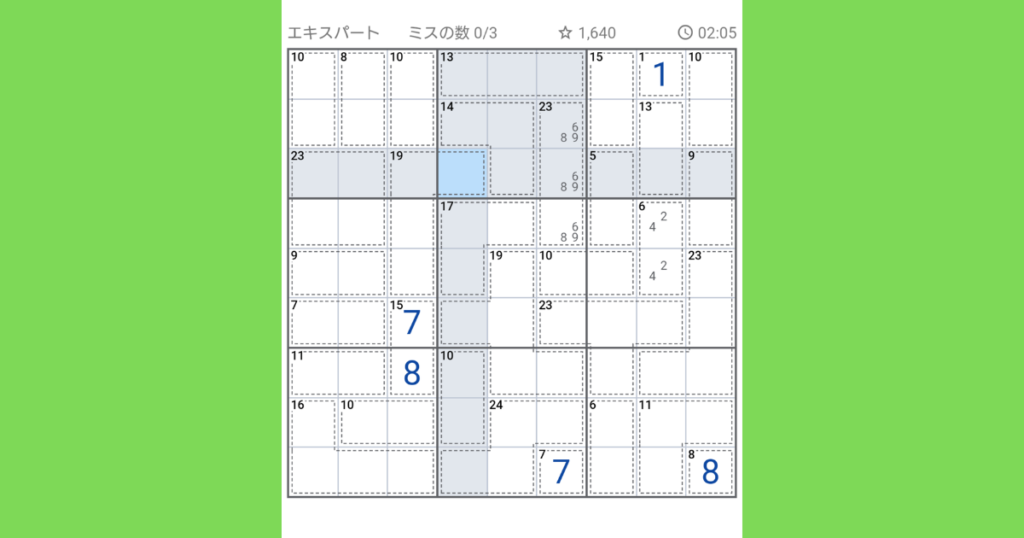
次に、左上と左中のブロックに注目します。2ブロック分なので45×2で90が合計になります。
この中で【19(4マス)】の1マス分だけ外のブロックに飛び出ていますが、ここだけ差額で計算できます。【10(2マス)】【8(2マス)】【10(2マス)】【23(4マス)】【9(2マス】【7(2マス)】【7】と、【19(4マス)】があります。
全部で10+8+10+23+9+7+7+19=93、ここから90を引いて3になります。
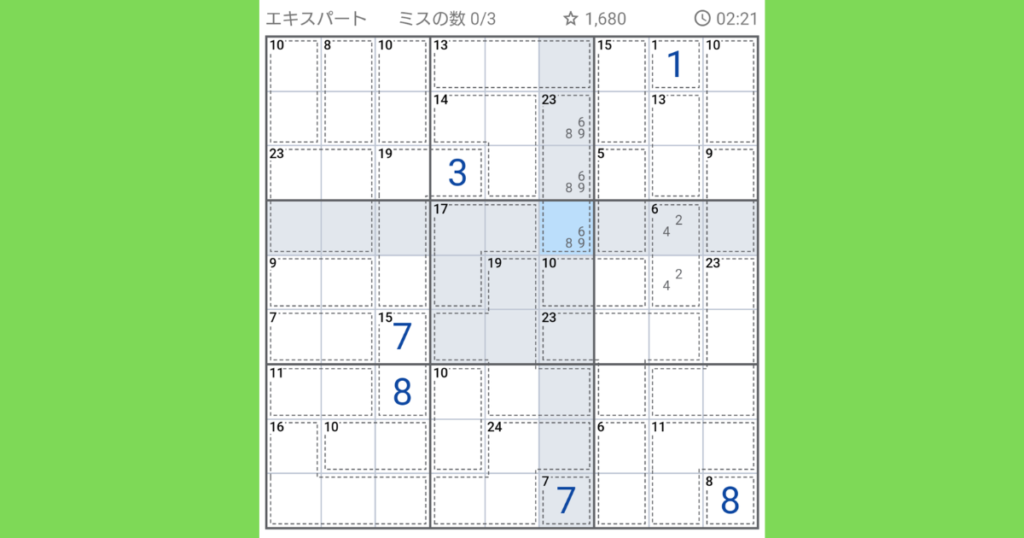
今度は上段真ん中のブロックから1つだけ飛び出ているマスに注目します。3が分かったので、13+14+3+23=53、ここから45を引いて8が入ります。
左上ブロックの【10(2マス)】ですが、この中に入るのは(1,9)、(2,8)、(3,7)、(4,6)のいずれかですが、縦と横に1,7,8があるので(4,6)のみになります。
同じ縦列で、下の2マスは45-(10+16+15)=4になり、4は(1,3)の組み合わせしかあり得ない。
同じ縦列の【19(4ブロック)】残り3マスには、既に入っている1,3,4,6,7,8以外の数字(2,5,9)が入ります。
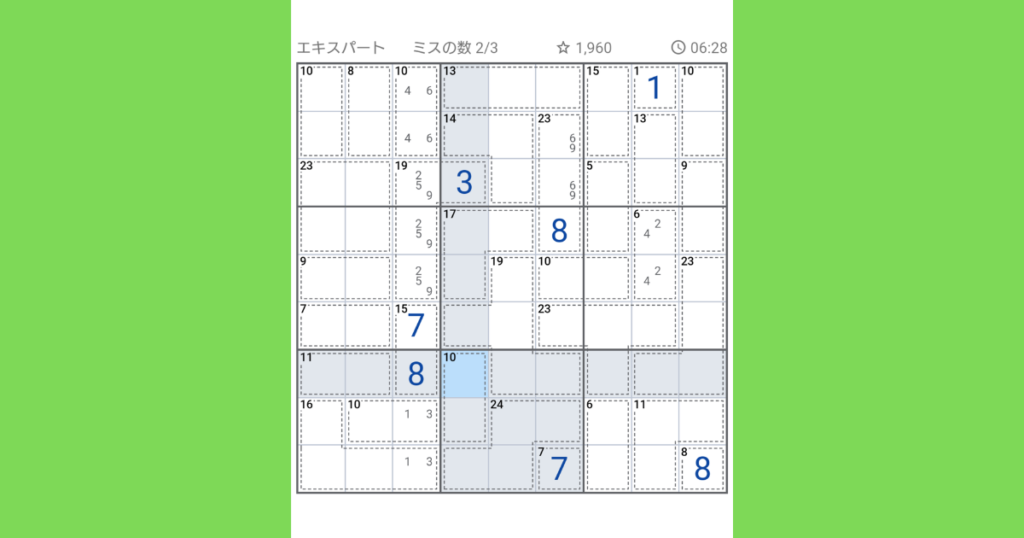

ここでウチの4男の手助け?により、気づいたら3ミスしていました。
今度は、一番下と下から2番目の横2列に注目します。そこから【10(2マス)】の上マスだけ飛び出ています。1列の合計は45,2列だと90になるので、
16+10+24+7+6+11+8+10=92、ここから90を引いて2が入ります。
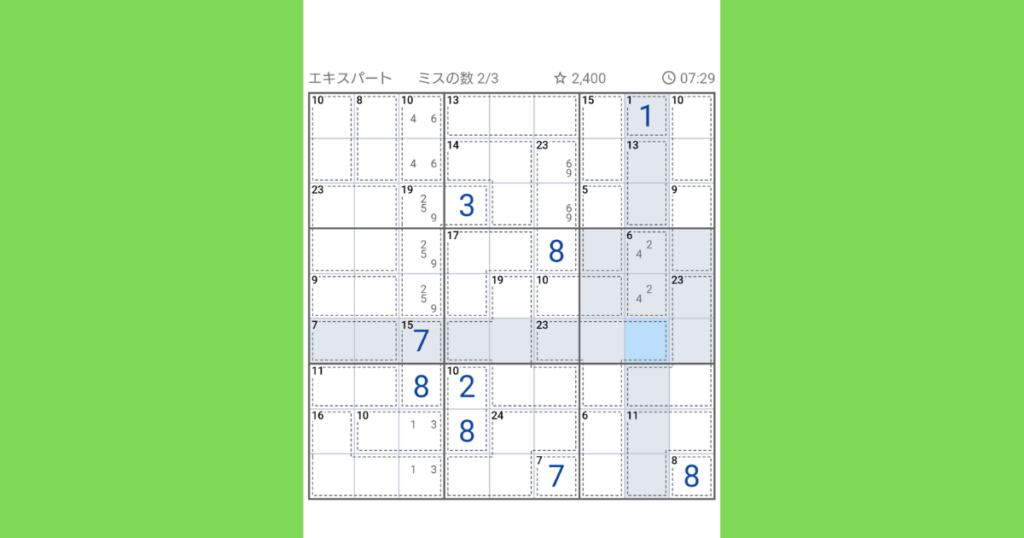
次に一番右、一番右から2番目の縦列に注目します。選択したマスだけ凹んでるので、ここを求めていきます。
90-(1+10+13+9+6+23+11+8)=9となります。
次はポイントですが、先ほど入れた9が真ん中の列に入っているので、右上と右下ブロックには右の列か左の列いずれかに9が入ります。
しかし、右の列に9が入る所は下から3番目のマス以外あり得ません。
右上の【10(2マス)】に9を入れると残りに1が入りますが、既に1が入ってます。【9(2マス)】と【11(3マス)】には9は入れません。11に入れようとすると9+1+1になってしまい、同じ数字は使えないからですね。中段のブロックには既に9が入っているので、下から3番目が9の入る場所となります。
すると右上ブロックに入る9は【15(2マス)】のみになりますので、(9,6)の組み合わせが入ります。
逆に1などの小さい数字も同じテクニックが使えて、【11(2マス)】の場合1は必ず入らなかったりします。
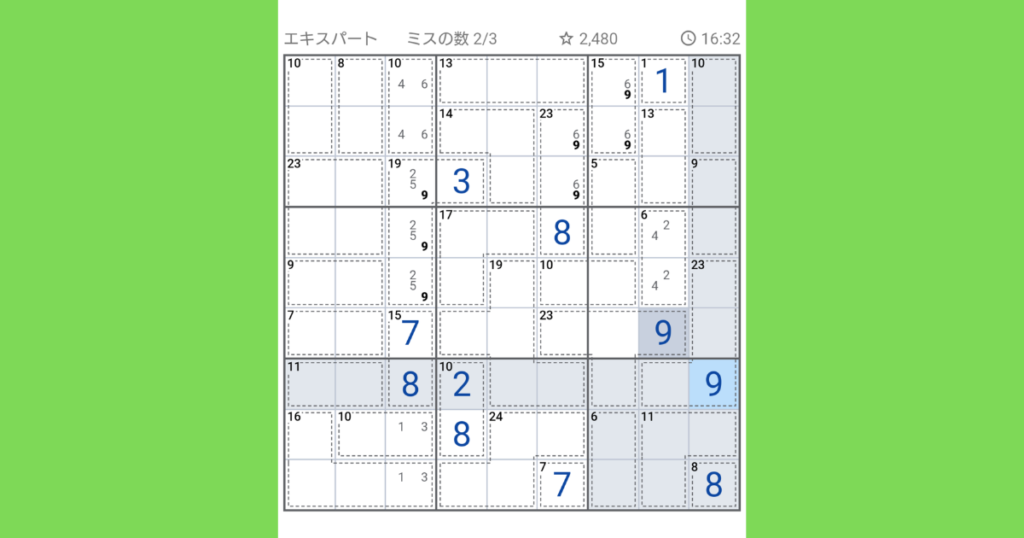
上の段にある【10(2マス)】と【15(2マス)】には必ず6が入ります。つまり、一番上と一列下には6が入る場所が決まっているので、真ん中にある【23(3マス)】の一番上に6は来ない事になります。なので真ん中のマスに6が入ります。
すると続けざまに数字を入れられます。
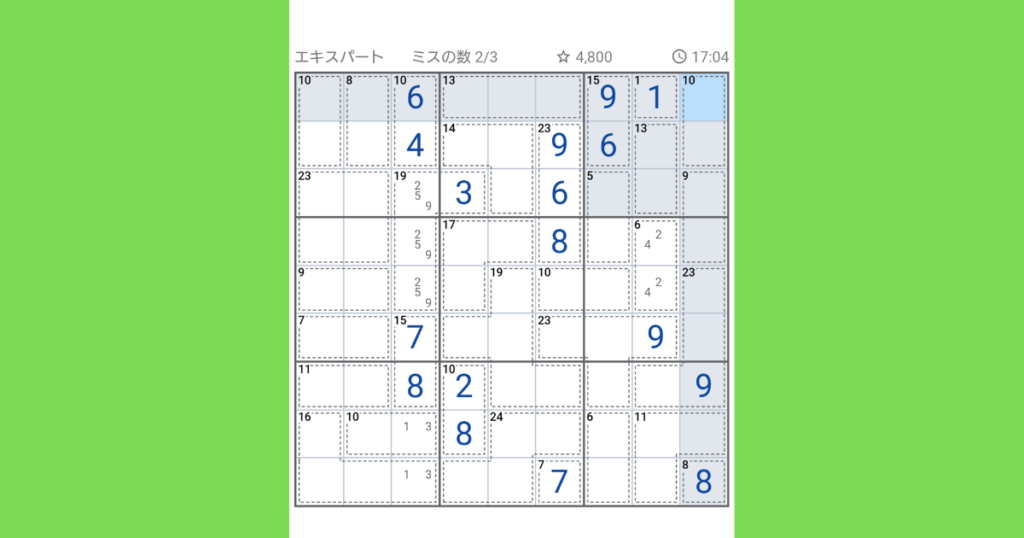
今度は右上の【10(2マス)】に注目して、入る数字の組み合わせは(1,9)、(2,8)、(3,7)、(4,6)のいずれかになりますが、既に1,6,9,8がありますので、(3,7)が正解になります。
その後、【13(2マス)】に注目して、(6,7)、(5,8)、(4,9)いずれかが入りますが、7,9が既にあるので(5,8)が入ります。
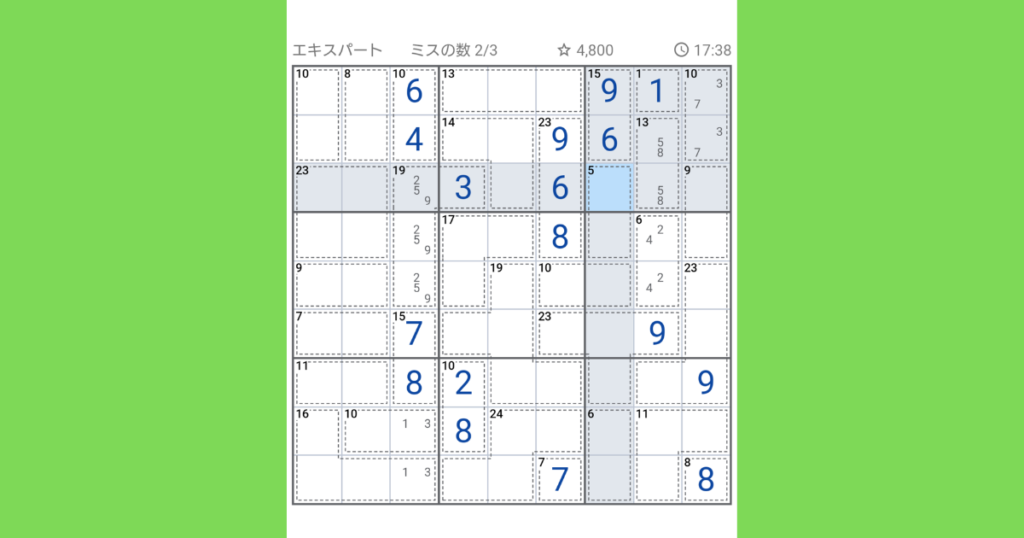
右上ブロックの残り2マスには2と4が入りますが、右下のマスに2を入れると、【9(2マス)】の中で7を入れる事になってしまい、既に7があるので2は入らないことが分かります。
なので右下に4,左下に2が入ります。
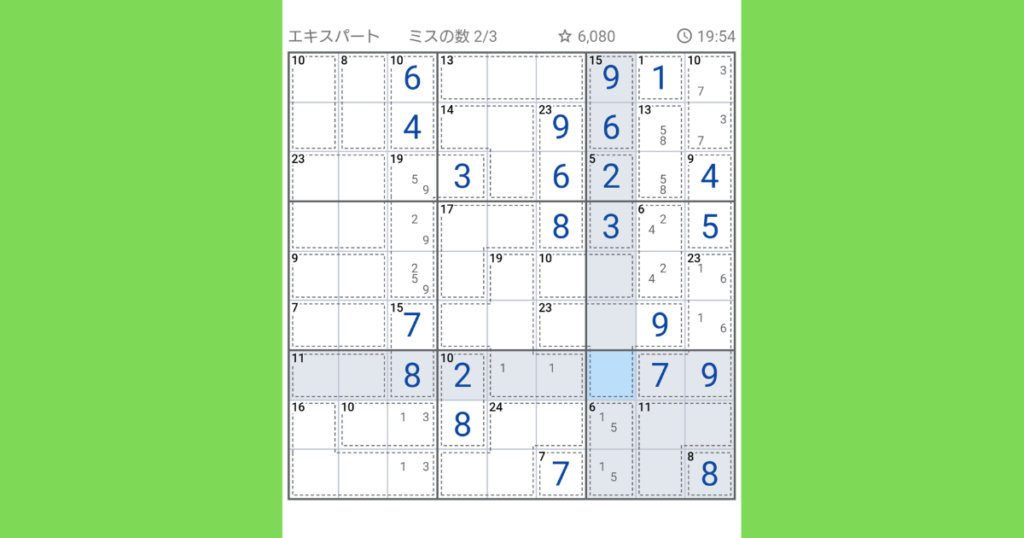
右下ブロックに注目して、45-(7+9+6+11+8)=4が残りのマスに入ります。
同じ列一番左側の【11(2マス)】には(5,6)、(4,7)、(3,8)、(2,9)のいずれかが入りますが、既に7,8,9があるので(5,6)が入ります。
同じ列にある残り2つのマスには残りの数字で1,3が入ります。
数字が埋まってくると段々楽になってきますよね!
左中段のブロックに注目します。この中で8が入るマスは【9(2マス)】しかあり得ません。
下の【7(2マス)】には8は入りきらず、上の列は隣のブロックに8があるので入りません。
【9(2マス)】の部分に8を入れると(8,1)となります。
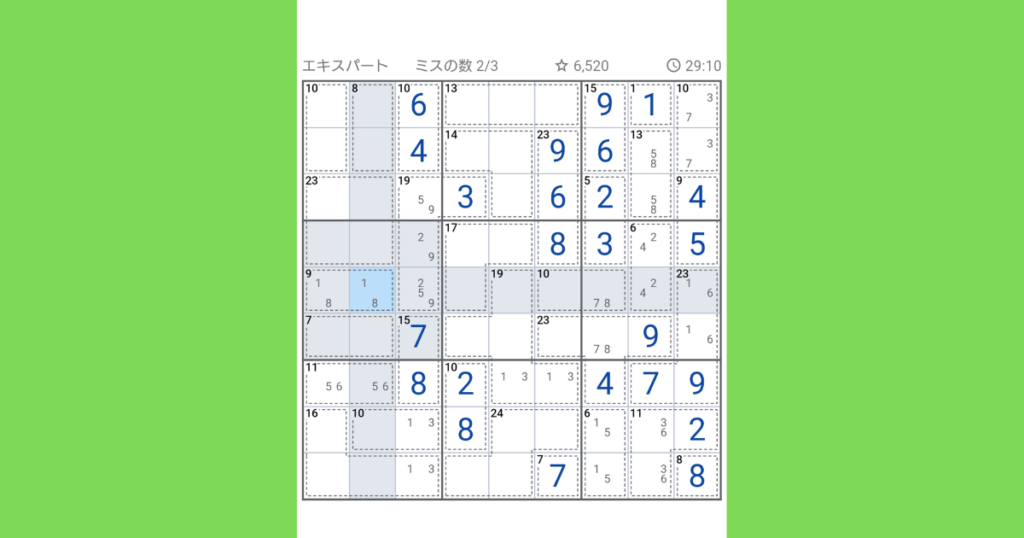
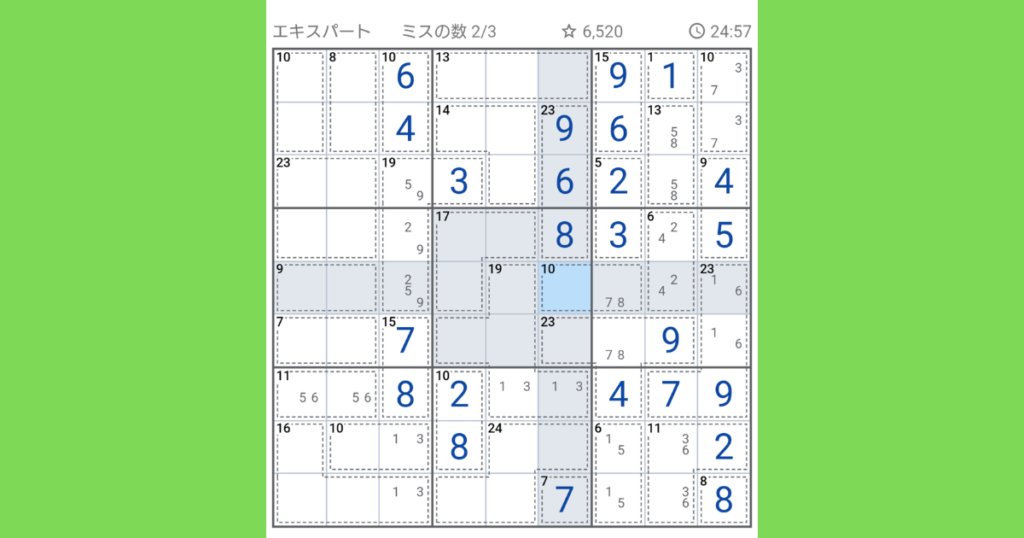
左中段ブロックの【7(2マス)】部分ですが、(1,6)、(2,5)、(3,4)のいずれかで、1と2は既に同ブロック内にありますので(3,4)が入ります。
そうすると、どこにも入っていない6が【23(4マス)】の下部分に入ります。
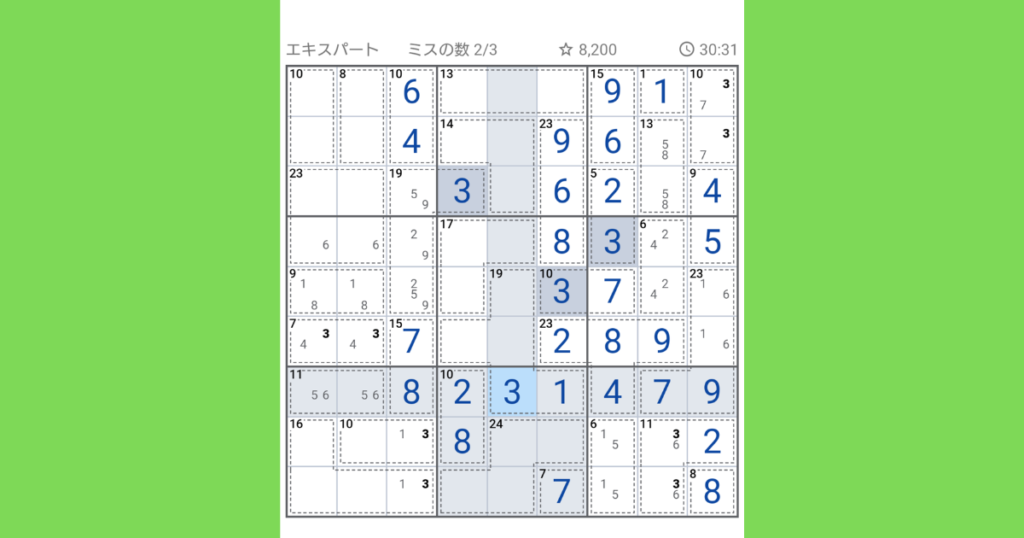
一番右から4番目の縦列に注目し、まだ入っていない4,5をマークしていきます。
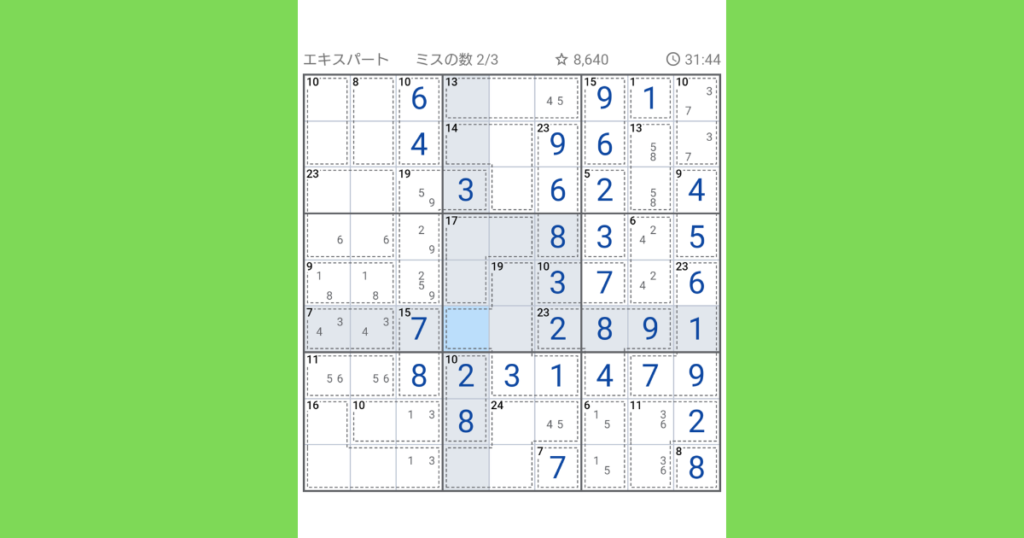
下から4番目の横列に、残りの数字5,6を入れていきます。
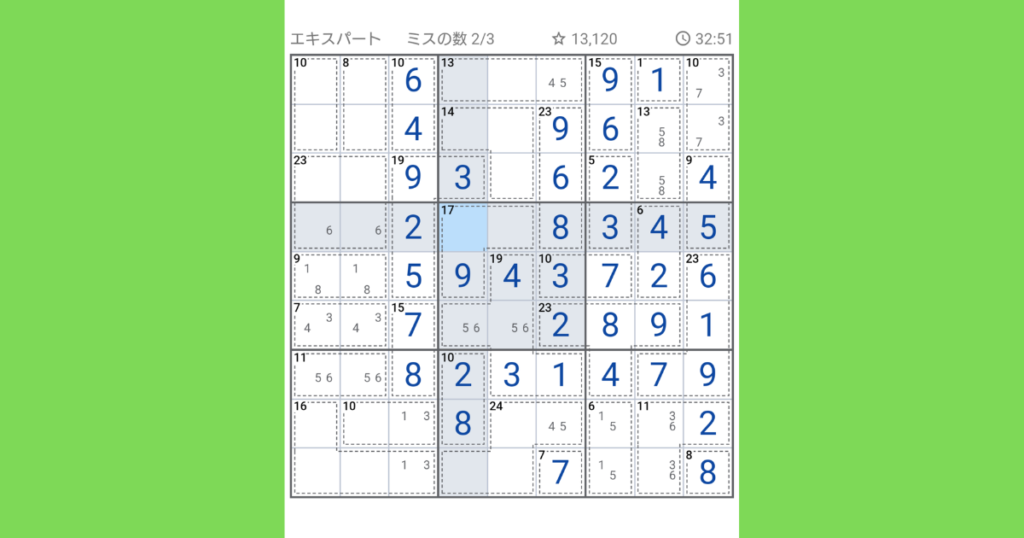
中央の縦列1番上と1つ下マスどちらかに2が入ります。(右上ブロック、真ん中ブロック、下ブロックに2がある為。)
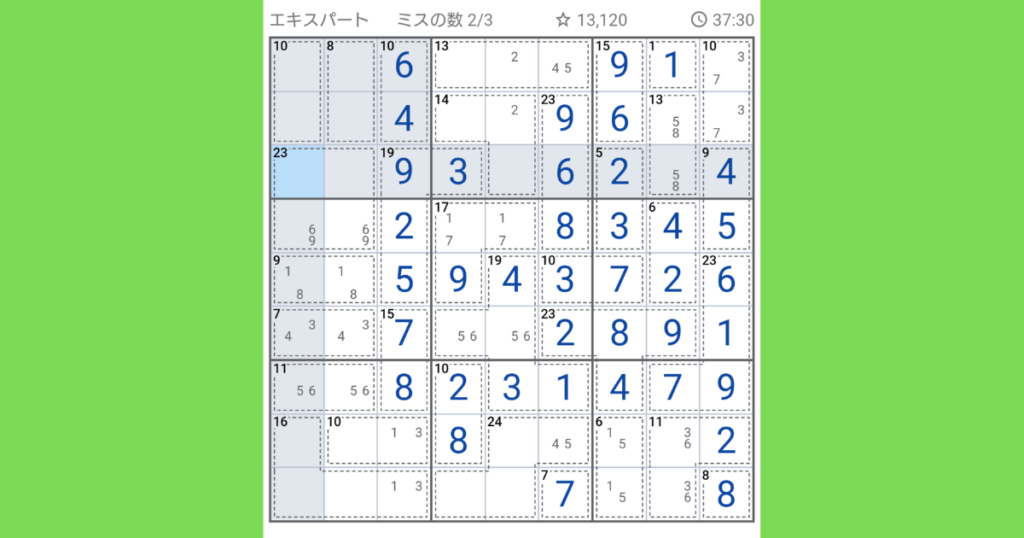
次に左上のブロックにある【23(4マス)】部分に注目します。下2マスに6,9(合計15)があるので上2マスは合計8になります。8になる組み合わせは(1,7)、(2,6)、(3,5)のいずれかになりますが、同ブロックに6,同列右側に3があるので(1,7)が入ります。
その後同じ左上ブロックにある【10(2マス)】には(2,8)、【8(2マス)】には(3,5)が続けて入ります。
【10(2マス)】に(2,8)が入ると、真下にある【9(2マス)】に入っている(1,8)が確定になり、左が1,右に8が入ります。その後【23(4マス)】上部の(1,7)も確定になり、左に7,右に1となります。
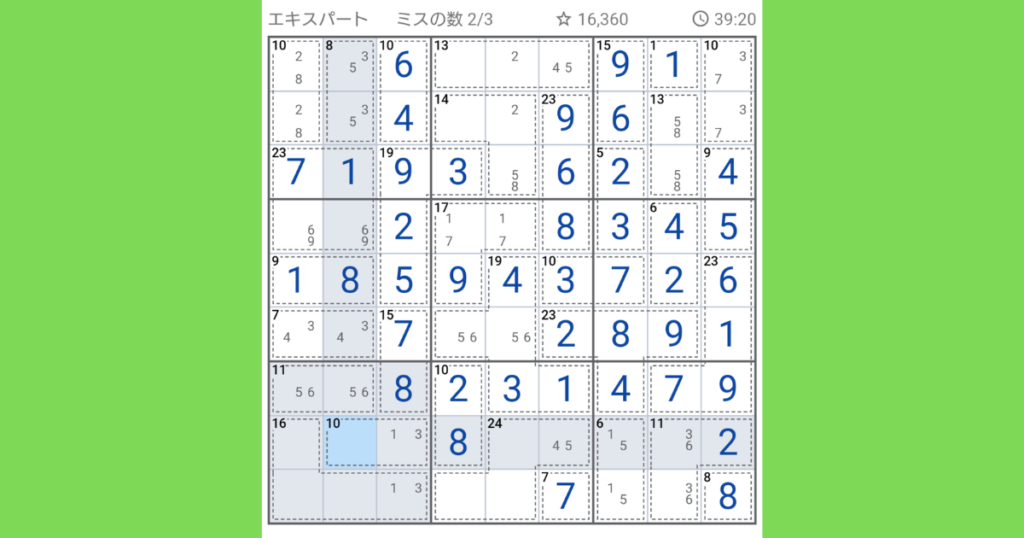
左下ブロックにある【10(2マス)】の左側に7が入ると、続け様に数字が入ってきます。

残りのマスにも数字を入れていき


ここまで来ればどんどん完成になります!

まだまだ修行が足りませんが、引き続き更新していきたいと思います。